VIRTUAL LAB
Telescopes
Approximately 3 hours (self-paced)
- Understand the Basic Principles of Telescopes
- Explore Different Types of Telescopes
- Investigate Optical Aberrations
- Conduct Practical Experiments
- Learn how to mitigate different types of aberrations
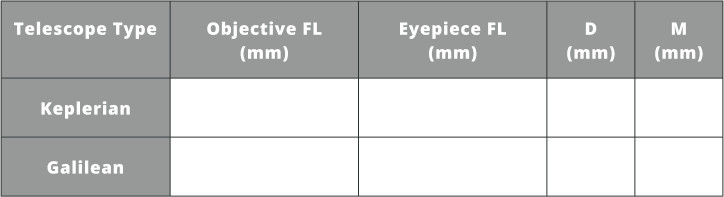
Telescopes can be used for both terrestrial and astronomical viewing. The difference mainly being their ability to magnify objects that are far away. Terrestrial telescopes, such as the Galilean telescope, can be used for observing objects on Earth and in our solar system but are not suited for viewing galaxies. Astronomical telescopes, on the other hand, are able to generate large angular magnifications that allow viewing of the most distant astronomical objects.
Basic Principles of Telescopes
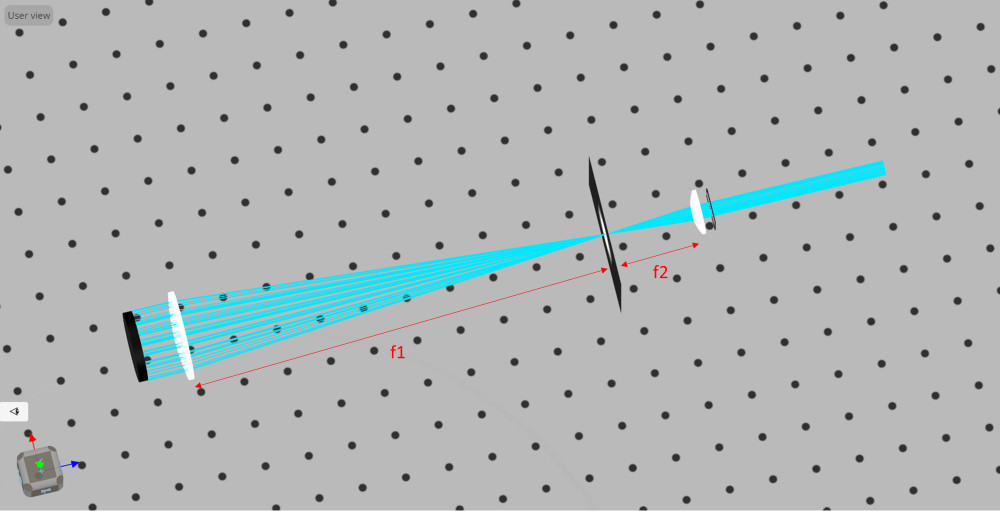
Telescopes, whether refracting or reflecting, operate on fundamental principles involving an objective lens or mirror to gather and focus light and an eyepiece lens that re-collimates the output. The focal lengths of the objective and eyepiece lens influence magnification, and different eyepieces can be used for varying magnification levels. The entrance aperture, diameter of the limiting element such as the objective, impacts the amount of light collected, affecting brightness and detail in images. The exit aperture, where the eye is placed, is located after the eyepiece, where the fields of view meet in a Keplerian telescope. In a Galilean telescope, this is inside the telescope due to the diverging light the negative lens produces. The position of the eye after the eyepiece lens is known as the eye relief.
The angular magnification is a function of the lenses used and is due to the change in angle of the input light from the source and the output light that enters the eye or camera. The negative sign is convention for determining if the image is inverted or not.
Telescope Parameters

- Using equations 1 and 3 from the previous section, fill out the table
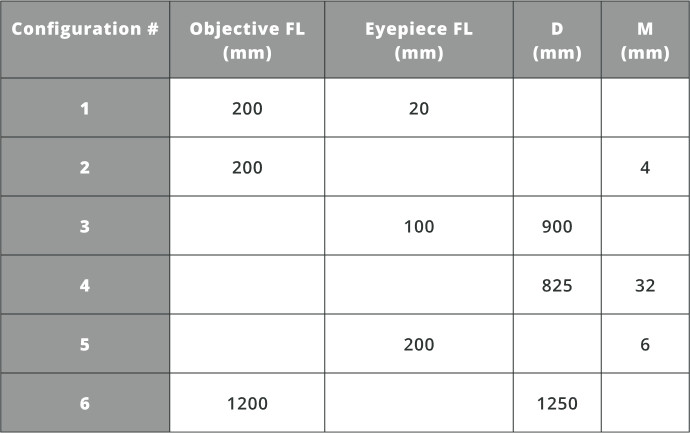
- Depending on what the purpose of the telescope is these parameters can be varied to conform to the needed performance. However, there are no independent variables, so changing one parameter, such as the focal length of the eyepiece, necessarily changes the others.

- Import the file “Refractive_Telescopes.opt” into the 3DOptix app
- Click on the Keplerian objective lens and determine the BFL at the wavelength used in the Kepler LS1
- Repeat this for the Keplerian eyepiece lens, but for the FFL (ignore the negative sign)
- Record the total distance, D, that needs to separate the objective and eyepiece lens
- Calculate the magnification, M, using equation 3
- Repeat the above steps for the other design, the Galilean telescope
- Next find the exit pupil location. This is where the three Keplerian LSs after the eyepiece lens cross and the spatial size is minimized. Do this by moving the detector and measuring the spatial size of the light field using the measure mode tool.
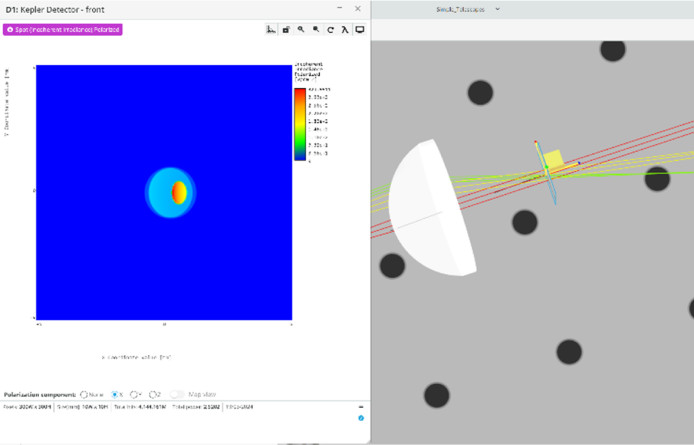
- Record this value in the table
- Finally, the angular resolution will be determined. Add a paraxial lens 25 mm in diameter with a focal length of 25 mm where the Keplerian and Galilean detectors are positioned
- Reference and position the detectors 25 mm from their respective paraxial lenses
- Reduce the detector size to 2×2 mm
- Using LS2 for both telescopes reduces the Y-angle until the two spots are overlapping. Click between the spots in the analysis window to bring up the cross section and confirm that the spots overlap
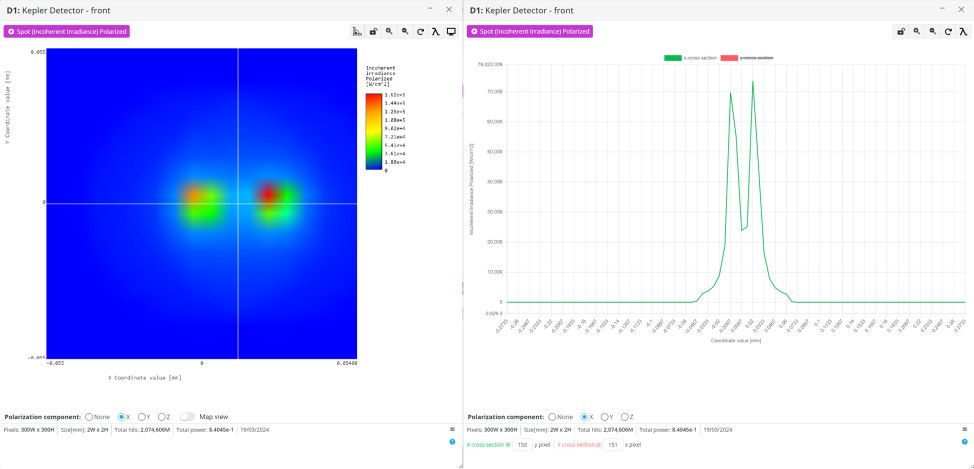
- Record this angle
- We now have the important parameters for both the Galilean and Keplerian telescopes
- Keep the simulation file open for the next exercise

- The exit pupil is also the eye relief of the system. A longer eye relief can be better as small movements of the eye when viewing do not move it appreciably out of the ideal viewing location. The angular resolution will be our limiting factor for observing very close objects such as binary star systems, and smaller is always better.
Early telescopes were characterized by their relatively small apertures and low magnification capabilities compared to modern telescopes. These early instruments were often constructed with simple wooden or metal tubes and lacked the sophisticated optical coatings and precision machining techniques used in contemporary telescope manufacturing.
Despite their limitations, early telescopes revolutionized our understanding of the universe and paved the way for advancements in astronomy and scientific inquiry. They played a crucial role in disproving the geocentric model of the universe and supporting the heliocentric model proposed by Nicolaus Copernicus. Over time, telescope designs evolved, leading to the development of more sophisticated optical configurations, including reflecting telescopes and compound telescopes, which combine lenses and mirrors.

- Import the file “Refractive_Telescope_Chromatic.opt” into the 3DOptix app
- Go to the analysis portal and run analysis
- Click on the analysis window
- In the analysis window, select each wavelength individually and measure the spot size for all the wavelengths using the measure mode tool
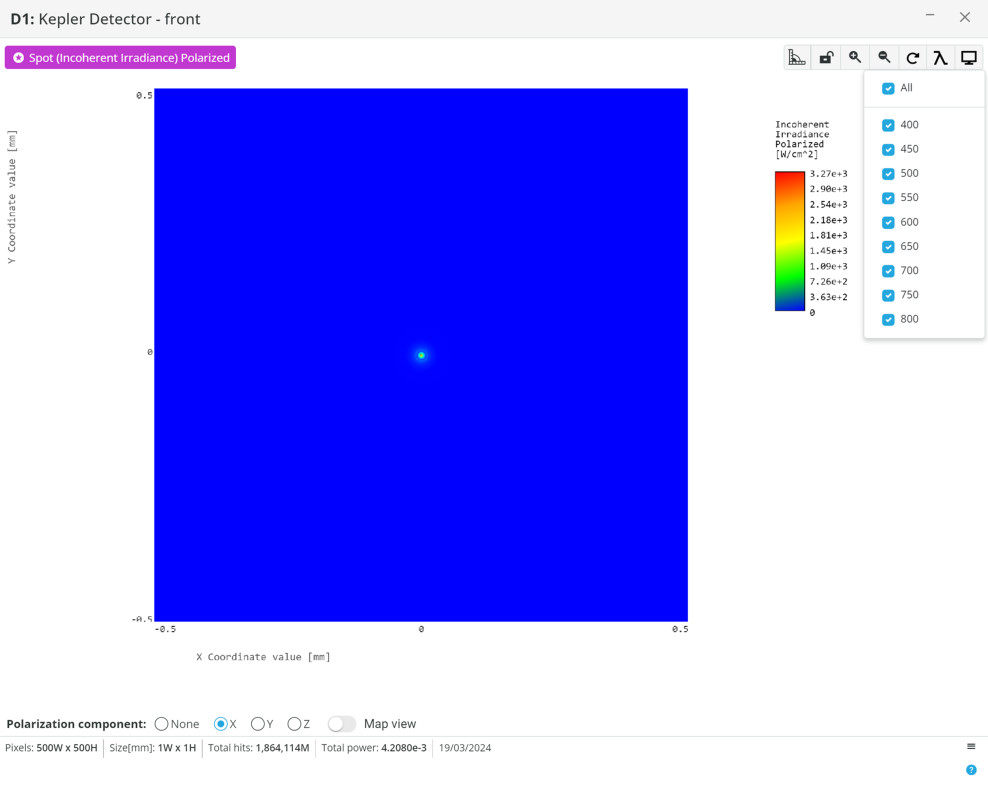
- The difference in spot sizes at the focal plane will appear as a halo of colors corresponding to the mismatching of the indexes of refraction.
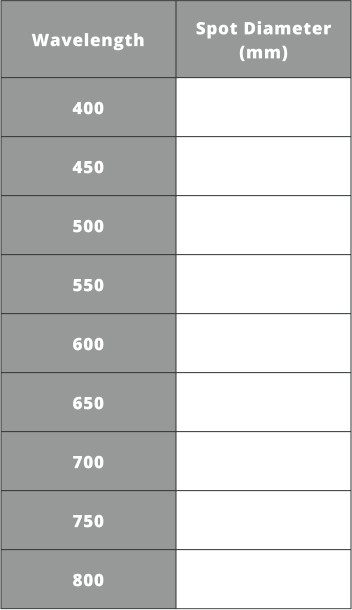
- By using different lens focal lengths and optical substrates we can reduce the spot size variation at the image plane. This will help keep this aberration type small.
There are two main types: longitudinal, which affects the convergence of different colors at the focal plane, and lateral, which causes color fringes around object edges. This aberration can degrade image quality, reducing sharpness, contrast, and color accuracy.
To mitigate chromatic aberration, optical designers use techniques such as apochromatic lens designs, employing extra-low dispersion glass. While chromatic aberration is a common challenge in optical systems, advancements in lens design and technology have enabled effective mitigation strategies in modern optical instruments.
Reflecting Telescopes
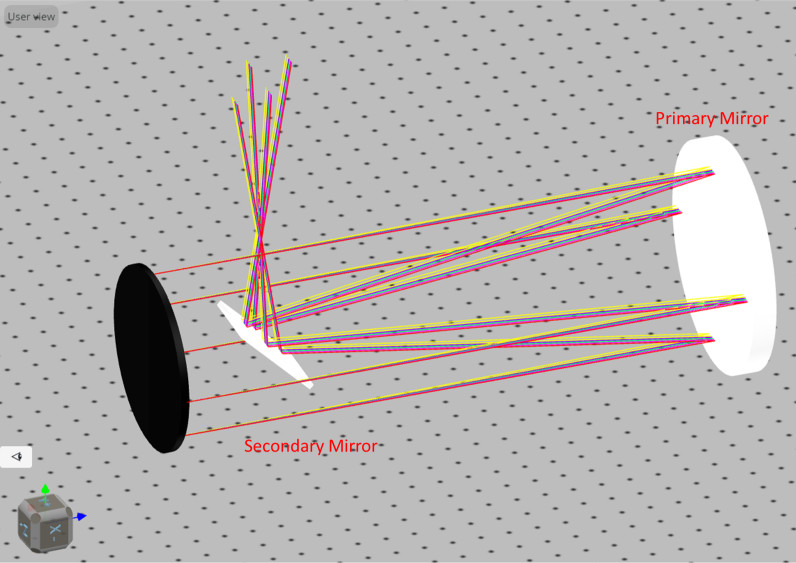

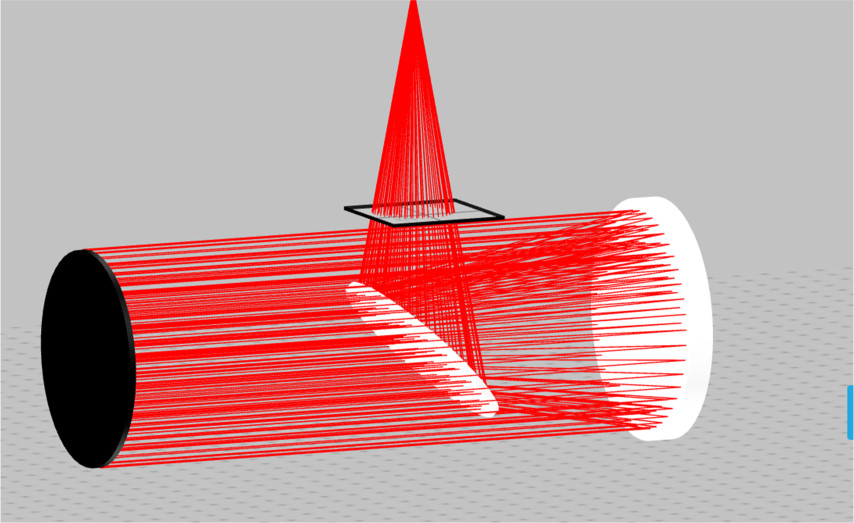
- Import the file “Reflective_Telescope.opt” into the 3DOptix app
- The first task is to determine the light throughput for different sizes and positions of the secondary mirror. Go to the analysis portal and run analysis.
 Ensure you select None for the polarization component to record the total power on the detector
Ensure you select None for the polarization component to record the total power on the detector
- Record the power in the table for configuration 1
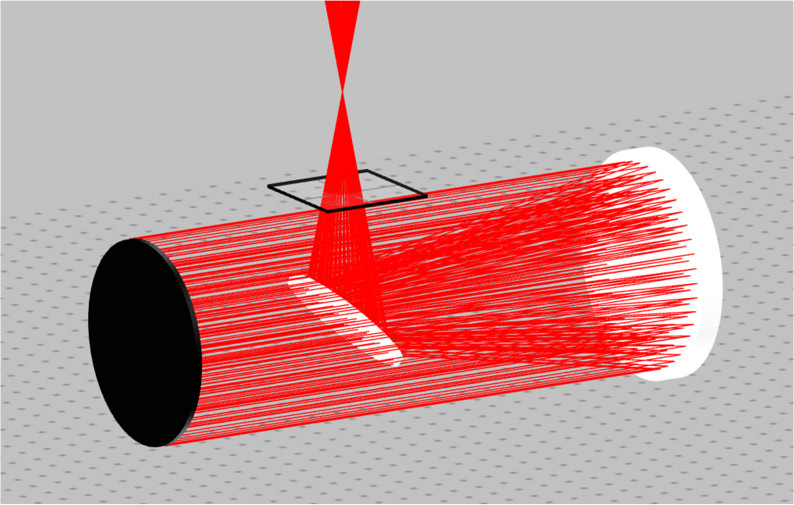
- Next, change the size of the elements to increase the light throughput
 Secondary Mirror Diameter = 120 mm
Secondary Mirror Diameter = 120 mm Secondary Mirror Position, Y = 95, Z = 200
Secondary Mirror Position, Y = 95, Z = 200
- Record the new power in the table for configuration 2
- Change the secondary mirror for the final configuration
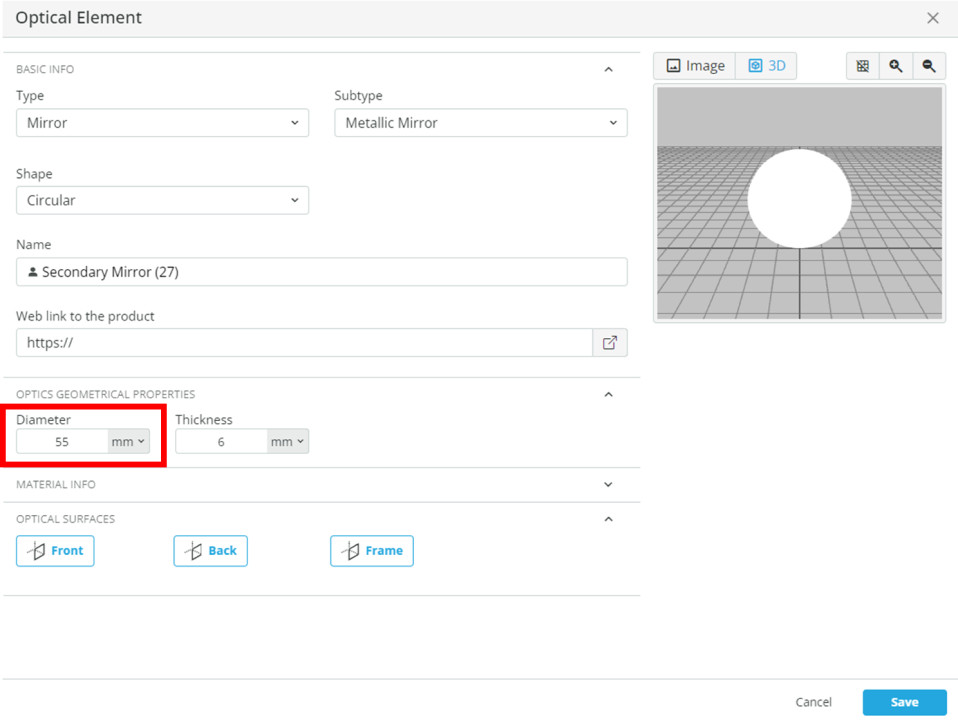
 Secondary Mirror Diameter = 55 mm
Secondary Mirror Diameter = 55 mm
 Secondary Mirror Position, Y = 97, Z = 100
Secondary Mirror Position, Y = 97, Z = 100
- Record the new power in the table for configuration 3.
 Notice in the third configuration that the focus is just outside the optical system
Notice in the third configuration that the focus is just outside the optical system
- Keep the simulation file open for the next exercise


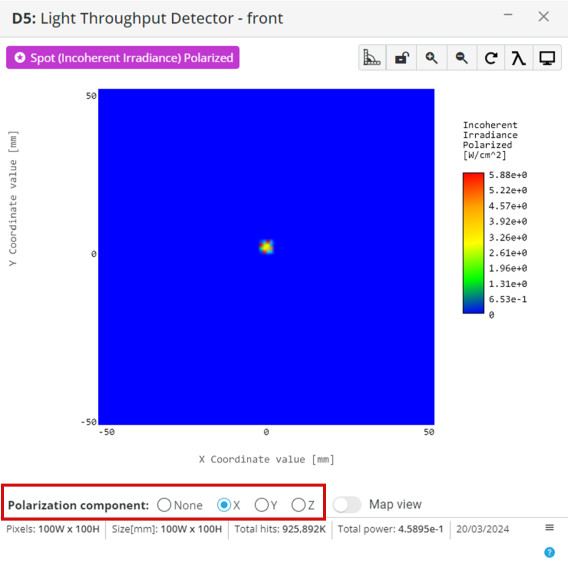
- With the Newtonian reflector in a nominal setup the secondary mirror can be further optimized to define the FOV. Add three light sources and place them collocated with Newtonian LS1.
- Name the light sources “Newtonian LS2”, “Newtonian LS3”, and “Newtonian LS4”.
- Change the light source angle to the following. We will define a 1.5 degree FOV.
 LS2: X Angle = 1.5 degrees
LS2: X Angle = 1.5 degrees
 LS3: X Angle = -1.5 degrees
LS3: X Angle = -1.5 degrees
 LS4: Y Angle = 1.5 degrees
LS4: Y Angle = 1.5 degrees
- Select the secondary mirror and make the front surface a detecting surface by clicking on it.
- Go to the analysis window and change the secondary mirror detector.
 Spot (Incoherent Irradiance) Polarized
Spot (Incoherent Irradiance) Polarized
 1e6 light source rays
1e6 light source rays
 300×300 pixels
300×300 pixels
- Run analysis and click on the analysis window to bring it to its own window.
- Notice the secondary mirror is now too small to capture the light from all source angles fully.
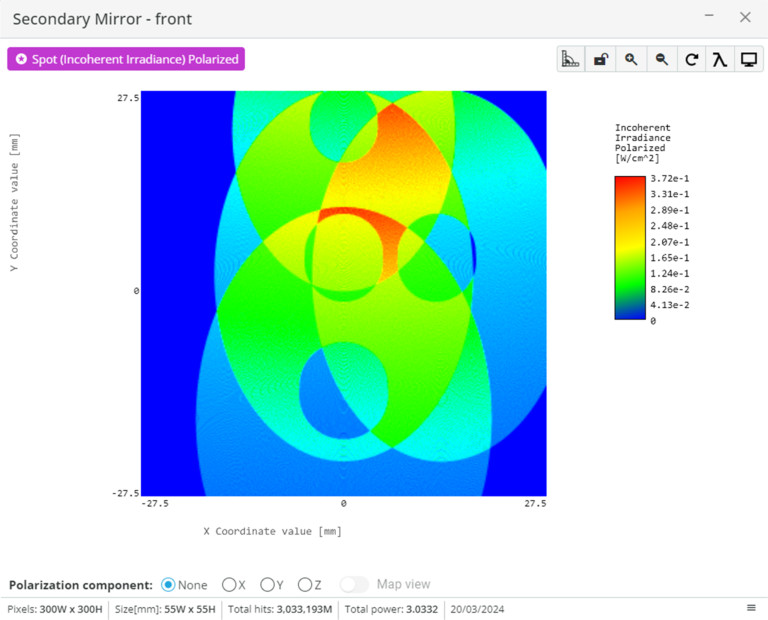
- Click on the secondary mirror, select settings, and change the diameter. Repeat this while re-running the analysis until the light from all light sources is incident on the mirror.
 Note that you may need to change the Y position of the mirror to both minimize the secondary mirror size and capture all the light
Note that you may need to change the Y position of the mirror to both minimize the secondary mirror size and capture all the light
- Compare the light throughput of the final configuration to configuration 3 in the table from exercise 4.
- Keep the simulation file open for the next exercise.

- The final piece of the Newtonian reflector is to insert an eyepiece and determine the magnification. Equations 1 and 3 determine the separation between the primary mirror and eyepiece, and the magnification is the same as for the refracting telescopes.
- Insert the eyepiece lenses from the optical catalog from the table below and fill in the missing information.
 Note that the equation 1 distance is the folded path from the primary mirror to the secondary mirror and from the secondary mirror to the focus
Note that the equation 1 distance is the folded path from the primary mirror to the secondary mirror and from the secondary mirror to the focus
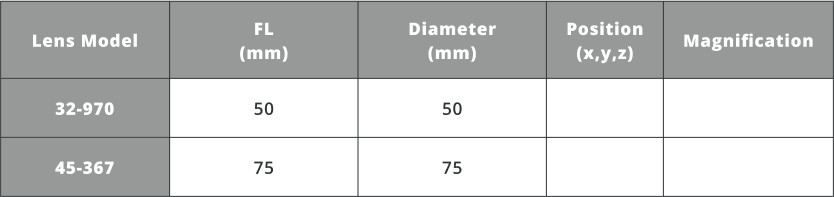
- Greater magnification also reduces the FOV which is a tradeoff for this system parameter. If viewing a planet in detail is desirable we would want a larger magnification, but if we want to see multiple galaxies we would need a larger FOV and therefore a smaller magnification.

- Import the file “Reflective_Telescope_Coma.opt” into the 3DOptix app
- Go to the analysis portal and run analysis
- Click on the analysis window to bring it into its own window
- In the analysis window select each source angle individually and observe the shape of the spot
- Change to logarithmic view to more easily see the coma present in the output
- Determine if the comatic aberration linearly increases with the source angle by measuring the horizontal and vertical dimensions by filling out the table.
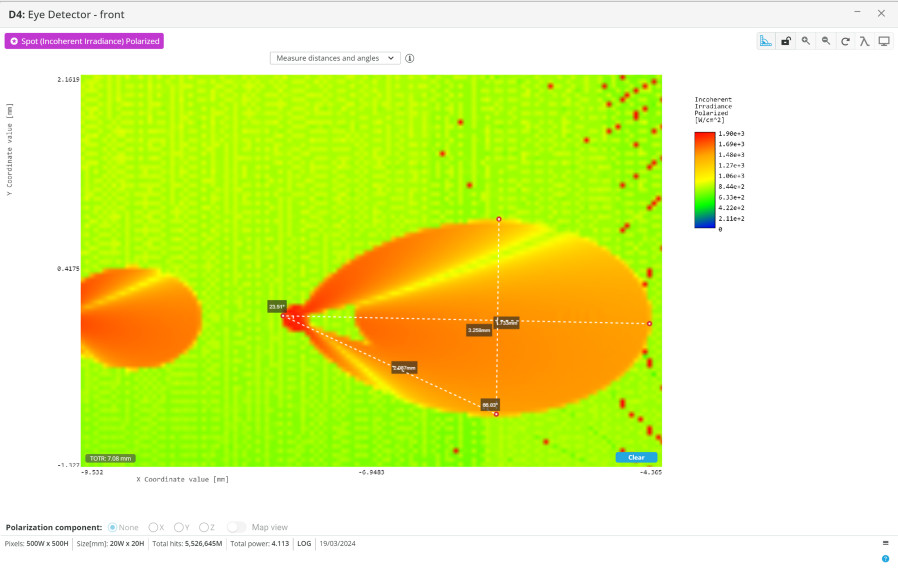
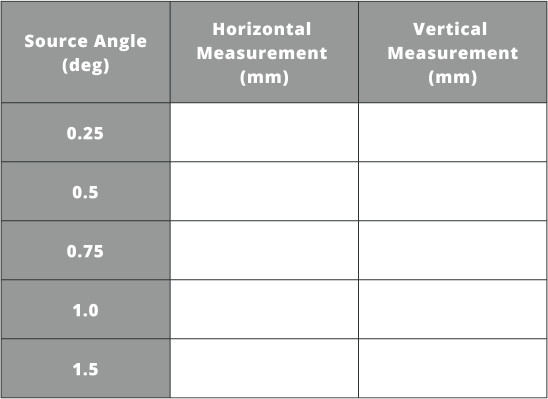
- The numbers measured for the table above simply show that the coma is greater at larger incident angles as they hit the parabolic mirror. Aberrations are more easily analyzed when compared to multiple optical systems to compare relative performance, or when using a camera with a specific pixel pitch. If the aberration, or sum of aberrations, creates a spot larger than the pixel pitch of the camera, then you can expect performance degradation.
Below are some references for telescope types and some additional educational information





